Apparently, according to the BC Curriculum, children in grades K-5 are too young to learn Computational Thinking and Robotics. Or at least, anything explicitly called that. When I enter those search terms into the Search Curriculum page, with parameters set to K-5, I’m given nothing! When I remove the parameters, I see that the terms begin showing up in Grade 6 and are most predominant in Secondary grades. What a disappointment!
But what is computational thinking (CT) and how does it link to robotics? Is it possible that these skills are, in fact, taught at the K-5 levels, though not explicitly called that?
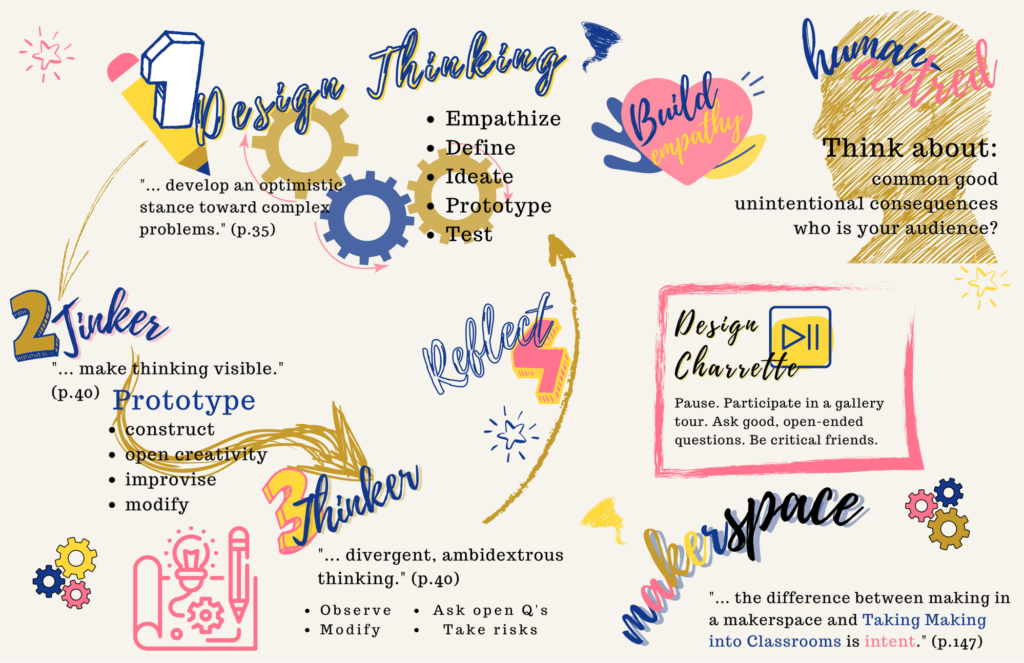
According to the CodeBC Computational Thinking Illustrated, when we engage in CT what we are doing is “specifically looking at what happens when we collect, store, and process data…. we take note and measure how data is transformed. We look at how information is processed and what is accomplished by that processing.” Another big part of CT is actually getting our hands busy by building and producing computational artifacts – like machines or robots. In other words, when we engage in CT, we do things like ideate, build, tinker, observe, and reflect. Now this is starting to sound like familiar curriculum for K-5.
When engaging in CT, we are also building skills in abstraction. One of the ways this is done is by building models – separating out the qualities we care about and leaving the rest. According to CodeBC, “when we deliberately separate our system into parts that can be individually understood, tested, reused, and substituted, then we are creating new abstractions.” Models can be physical objects or something less tangible, like a computer program. It takes time to learn how to narrow the margins and scope of a model so that the variables are measurable – create something without boundaries and you’ll “end up simulating the whole world!“
In CT, we are also guided to build skills in analysis, problem-solving, and communication (with machines, computers and humans). The answers we get after analyzing results may not always be obvious to others, and so it is our task as computational thinkers to figure out how to translate our findings into clear and accessible terms. Inversely, we may have an idea that we want to test out and we must also learn to translate our ideas into CT: coding, programming, machinery, etc.
In K-5, we are asked to build and analyze models, solve simple and complex problems, and learn how to communicate with ourselves and others. A great deal of this is done through play and scaffolding emerging scientific, mathematical, social, physical and creative thinking skills.
Team-work is another skill developed with CT. CodeBC reminds us that “building any complex system, software or hardware, requires more work be done in less time than any single person can accomplish.” Adding more people isn’t the magic recipe, however; “interpersonal and communication skills as well as knowledge of different team methodologies and processes” are vital to effective teamwork, as is good management as teams expand.
As it turns out, we are continuously developing CT skills at the K-5 level; it’s just not explicitly called CT. Being aware of the end-goal might be helpful for teachers who are introducing the skill-building exercises that will prepare children to become computational thinkers.
So, what are some explicit ways we can engage in CT?
Decomposition is one. Taking apart objects or breaking down a process into individual steps, like Josh Darnit does in his PB&J Exact Instructions Challenge:
Primary teachers are very familiar with another exercise in CT: pattern recognition. According to CodeBC, “forming an idea of what you expect is one way to find patterns. The more you look, the more patterns you will find in nature, in computational artifacts, and in processes. When we recognize a pattern, we can use our other computational thinking skills to help us understand its importance.“
Once we start to find and recognize the patterns that surround and are within us, we must learn to describe the patterns we see with precision. For this, we learn pattern generalization and abstraction. When generalizing, we look for similarities or commonalities in a group of patterns and we try to describe them in a way that is both clear and efficient. When we learn to describe a group of patterns, or a pattern of patterns, all at once, then we have an abstraction.
Finally, CT skills can be explored using algorithm design. While some algorithms are computer programs, it’s fair to say that an algorithm is more like an idea. In order to design an algorithm, you need to think about what you want to accomplish (your goal), and what tools and limitations you have (the constraints of the system). CodeBC says that designing an algorithm that “accomplishes specific goal within the constraints of the system is like creating an elegant dance that everyone else wants to learn.” Just like a dance, this is a process that can be explored, played with, and scaffolded in K-5.
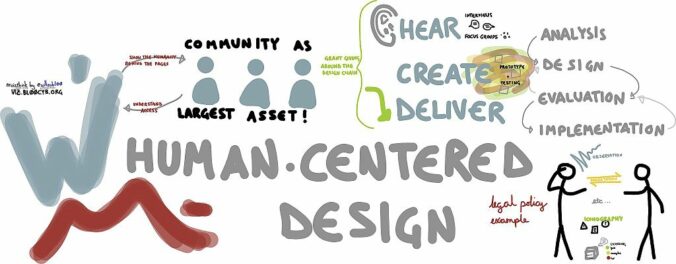
So, what do CT and robotics have in common? CT is the framework we need in order to engage in robotics. It is the exploration and skill-building of language, patterning, process, and thinking that makes something like robotics possible. While “Computational Thinking” and “robotics” may not show up in the K-5 BC Curriculum, the foundational building blocks are there: analyzing, communicating, ideating, pattern-recognition, problem-solving. We just have to learn how to read the language of CT and remember to begin with the end in mind.


Recent Comments